Flächenträgheitsmomente

Das polare Trägheitsmoment 2. Grades ist Ip = Iy + Iz, sofern der Bezugspunkt des polaren Flächenmomentes im Schnittpunkt der y- und z-Achse liegt.

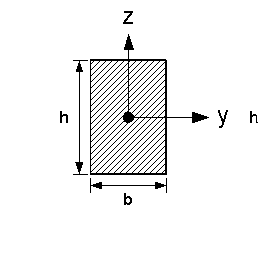
Rechteck

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

Flaechentraegheitsmoment
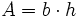A = {b cdot h }
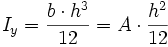I_y = {b cdot h^3 over 12} = A cdot frac {h^2} {12}

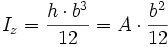I_z = {h cdot b^3 over 12} = A cdot frac {b^2} {12}

Das Quadrat kann als Spezialfall des Rechtecks mit b = h berechnet werden

Dreieck

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

Flaechentraegheitsmoment
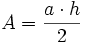A = frac {a cdot h}{2}
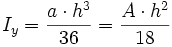I_y = frac {a cdot h^3}{36} = frac {A cdot h^2}{18}
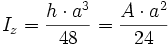I_z = frac {h cdot a^3}{48} = frac {A cdot a^2}{24}

Das Dreieck ist nur um die z-Achse symmetrisch

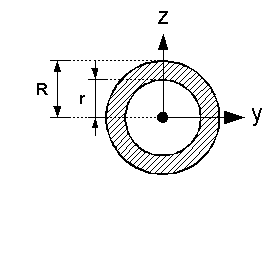
Kreisring

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

Flaechentraegheitsmoment
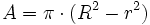A = pi cdot (R^2 - r^2)
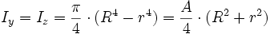I_y = I_z = {pi over 4} cdot (R^4 - r^4) = {A over 4} cdot (R^2 + r^2)

Der Kreis kann als Spezialfall des Kreisrings mit r = 0 berechnet werden.

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse
Ellipsenring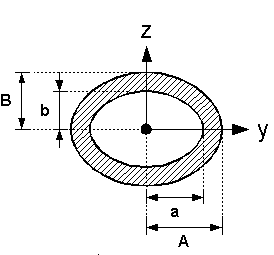

Flaechentraegheitsmoment
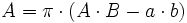A = pi cdot (A cdot B - a cdot b)
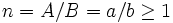n = A/B = a/b geq 1
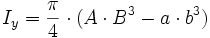I_y = frac {pi}{4} cdot (A cdot B^3 - a cdot b^3)

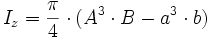I_z = frac {pi}{4} cdot (A^3 cdot B - a^3 cdot b)

Das Verhältnis  ist das Verhältnis der halben Achsen desEllipsenringes und muss bei der Berechnung des polaren Flächenmomentes für die Ellipse am Innenrand, gleich dem Verhältnis
der Ellipse am Aussenrand sein. Die Ellipse kann als Spezialfall des Ellipsenringes mit a = b = 0 betrachtet werden

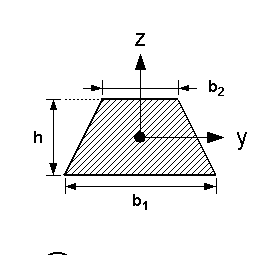
Symmetrisches Trapez

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

Flaechentraegheitsmoment
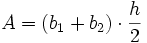A = (b_1+b_2) cdot frac{h}{2}
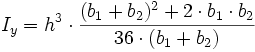I_y = h^3 cdot frac {(b_1 + b_2)^2 + 2 cdot b_1 cdot b_2}{36 cdot (b_1 + b_2)}
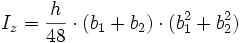I_{z} = frac {h}{48} cdot (b_1 + b_2) cdot (b_1^2 + b_2^2)

Regelmäßiges n-Eck

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

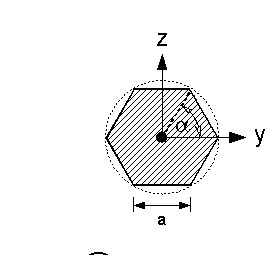Flaechentraegheitsmoment
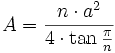A = frac{n cdot a^2}{4 cdot an frac{pi}{n}}
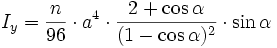I_y = frac {n}{96} cdot a^4 cdot frac{2 + cos alpha}{(1 - cos alpha)^2} cdot sin alpha

Iy ist um alle Achsen gleich

Kastenprofi

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse
l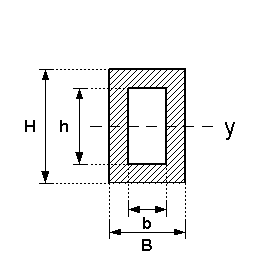
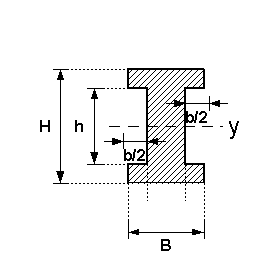
Flaechentraegheitsmoment		    

 

I-Träger

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

Flaechentraegheitsmoment
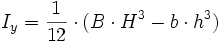I_{y} = frac{1}{12} cdot (B cdot H^3 - b cdot h^3)  		  
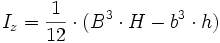I_{z} = frac{1}{12} cdot (B^3 cdot H - b^3 cdot h)

(Doppel-T-Träger)
-(nur für Profil 7; für Profil 8 und 9 gelten
andere Formeln)

C-Profil

Nr Fläche Axiales Flächenmoment 2. Grades um y- und z-Achse

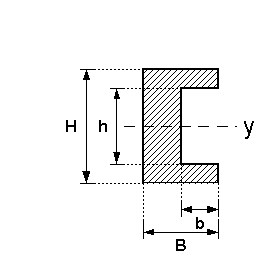Flaechentraegheitsmoment		    
InnoRat, Ingenieurbüro, Mechanical Engineering, Konstrukteure, Maschinenbau, Autodesk Inventor, Vorrichtungsbau, 3D Druck, Konstruktionsbüro

Haben Sie Fragen? Rufen Sie uns jederzeit an

Kontaktiere uns